Ano de 2025 de Nosso Senhor

 

𒁠𒁠𒁠    Primeiro semestre   𒁠𒁠𒁠

Variáveis Complexas 

Nesta disciplina estudaremos as funções de uma variável complexa, percorrendo, assuntos como: Noções topológicas do plano complexo; Funções unívocas e plurívocas; Funções holomorfas,  Sequências e séries numéricas e de potências, Série de Laurent e teoria dos resíduos.

Plano de ensino

Uma cópia pdf do Plano de ensino pode ser baixada clicando aqui.

 

Datas das Provas

Prova 01:  dia 13/06/25

Prova 02:  dia 22/08/25

Exame: dia 29/08/25

 

Lista de exercícios

• Lista 01 – Números complexos na forma algébrica.
• Lista 02 – Projeção estereográfica. Números complexos na forma trigonométrica.
• Lista 03 – Topologia no plano complexo.
• Lista 04 – Sequências em C.
• Lista 05 – Séries numéricas em C.
• Lista 06 – Funções de uma variável complexa.
• Lista 07 – Limite e continuidade de funções complexas.
• Lista 08 – Derivação complexa.
• Lista 09 – Integração em C.

Extras/resoluções

• Video contendo a resolução de algumas questões da lista 01, acesso  aqui . Atentamos apenas que, como este vídeo foi feito durante a pandemia, a numeração do enunciados pode estar diferente.
• Resolução de os exercícios da lista 02, sobre a projeção estereográfica, clique aqui
• Vídeo contendo a resolução de algumas questões da Lista 03, acesso aqui  Atentamos apenas que, como este vídeo foi feito durante a pandemia, a numeração do enunciados pode estar diferente.
• Vídeo contendo a resolução de algumas questões da Lista 04, acesso aqui  Atentamos apenas que, como este vídeo foi feito durante a pandemia, a numeração do enunciados pode estar diferente.
• Enunciado e gabarito de uma prova antiga, de 2010, acesso aqui.
• Resolução de alguns exercícios das listas 03,04 e 05, feitas no dia 02/06/25, acesso aqui.
• Vídeo de 2020, comentando um pouco mais sobre ramos. Acesso aqui.
• Video apresentado a resolução de algumas questões da Lista 06. Acesso aqui

Arquivos pdf das aulas 

Aula 01  (23/04/25) Números  complexos como um corpo. Propriedades aritméticas. Potências de i. Imersão de R em C. Forma algébrica e unidade imaginária. Conjugado e propriedades. Módulo e representação no plano complexo.

Aula 02 (25/04/25) Propriedades do módulo. A projeção estereográfica e o plano complexo extendido.

Aula 03 (30/04/25) Forma trigonométrica. Produto e quociente nessa forma. Fórmulas de De Moivre.

Aula 04 (07/05/25) Topologia em C: o conjunto dos  números complexos como um espaço métrico. Vizinhança e vizinhança perfurada. Ponto interior de um conjunto.  Fechados e abertos de C. Porto de acumulação de um conjunto e o derivado. Conjunto conexo.

Aula 05  (09/05/25) Relação entre fechado e aberto de C. Compactos de C e o teorema de Borel-Lebesgue.

Aula 06  (14/05/25) Fronteira de um conjunto. Sequências em C. Limite de sequência. Sequência limitada. Propriedades aritméticas das sequências.

Aula 07 (21/05/25) Subsequência. Ponto aderente a uma sequência e a um conjunto. O Teorema de Bolzano-Weierstrass. Fecho de um conjunto. Limite infinito.

Aula 08  (23/05/25) Sequência de Cauchy. Séries complexas numéricas. Principais resultados. Convergência absoluta. Testes da comparação e da razão.

Aula 09 (28/05/25) Funções de uma variável complexa. Funções unívocas e plurivocas. A função exponencial complexa.

Aula 10  (30/05/25) Propriedades da função exponencial. Representação na forma polar. Funções trigonométricas complexas seno e cosseno.

Aula 11 (04/06/25) Funções hiperbólicas complexas. A função Logarítmica complexa.

Aula 12 (06/06/25) propriedades da função logarítmica complexa. A função potência. Funções trigonométricas inversas.

Aula 13  (11/06/25) Aula de exercícios.

Aula 14 (18/06/25) Limite e continuidade de funções complexas.

Aula 15 (25/06/25) Derivação em C. Funções holomorfas. Equações de Cauchy-Riemann.

Aula 16  (27/06/25) Regras de derivação complexa. Conceito de função inteira. O teorema da regra da cadeia.

Aula 17 (02/07/25) Curvas no plano complexo.

Aula 18 (04/07/25) Integrais curvilíneas. TFC.

Aula 19  (09/07/23) Integrais  curvilíneas, parte 2. Teorema da primitiva.

 

 

 

𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰

Cálculo II (Matemática diurno)

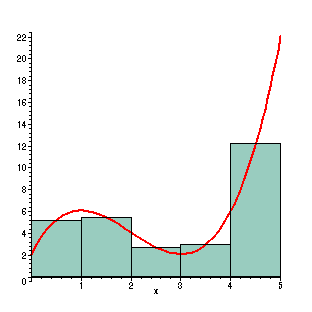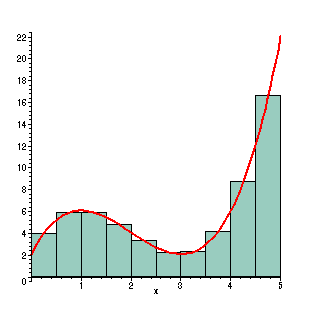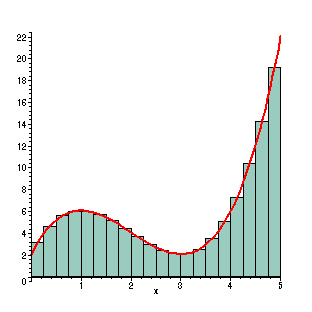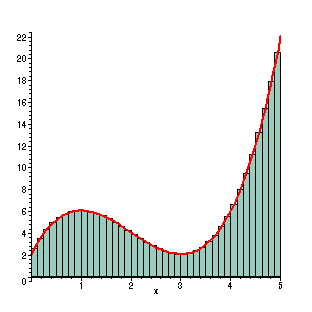
Dando continuidade ao estudo de Cálculo de funções de uma variável real estudaremos neste segundo curso de Cálculo o conceito de integral definida e o processo inverso à derivação, chamado de antiderivação, ou integração indefinida. O importante Teorema Fundamental do Cálculo, que faz a conexão entre este Cálculo e o anterior será estudado. Daremos ênfase a algumas aplicações da integral definida.

 

Plano de Ensino

Uma cópia pdf do plano pode ser baixada clicando aqui.

 

Datas das Provas

Prova 01:  dia 13/06/25

Prova 02:  dia 22/08/25

Exame: dia 29/08/25

 

Extras

• Vídeo ilustrando as aproximações por falta e por excesso, da área de uma região do plano, via somas de Riemann (extraído do Facebook, do grupo Math is Visual ). Acesso aqui.

 

Listas de Exercícios

• Lista 01 – Integral definida: primeiros conceitos.
• Lista 02 – O Teorema Fundamental do Cálculo. Integrais imediatas.
• Lista 03 – Constante de integração. Integrais imediatas.
• Lista 04 – Integrais envolvendo completamento de quadrado e substituição trigonométrica. Integração por partes.
• Lista 05 – Integrais de potências de seno e cosseno. Integrais por decomposição em frações parciais.

Arquivos das aulas

Aula 01  (23/04/25) Conjuntos limitados. Ínfimo e supremo de um conjunto. Funções limitadas. Partição de um intervalo e propriedades. Somas inferior e superior. Integrais inferior e superior.

Aula 02 (25/04/25) Função integrável. Um primeiro critério de integrabilidade. Exemplo de integração pela definição.

Aula 03  (30/04/25) outros exemplos de integração pela definição. Oscilação de uma função. Critério de Darboux. Propriedades da integral definida.

Aula 04 (07/05/25) Resolução de exercícios da List.a 01.

Aula 05 (09/05/25) Função de Lipschitz. Resolução de exercícios da lista 01.

Aula 06  (14/05/25) Função definida a partir da sua integral. O Teorema Fundamental do Cálculo (TFC), no primeiro formato e no segundo formato. Exemplos.

Aula 07 (21/05/25) Demonstração do TFC. Antiderivada. Primeiras regras de integração indefinida.

Aula 08 (23/05/25) Outras regras de integração indefinida.

Aula 09 (28/05/25) Formulas que envolvem v^2+-a^2. Completamento de quadrado perfeito para integrais da forma 1/(ax^2+bx+c).

Aula 10 (30/05/25) Integrais da forma (px + q)/(ax2+bx+c) e (px +q)/sqrt(ax2+bx+c).

Aula 11 (04/06/25) Integrais por substituição trigonométrica. Integração por partes.

Aula 12 ( 06/12/25) Aula de exercícios.

Aula 13  (11/06/25) Aula de exercícios, sobre a Lista 04.

Aula 13  (18/06/25) Aula de exercícios  da Lista 04.

Aula 14 (27/06/25) Integrais envolvendo potências de seno e cosseno. Integrais por decomposição em frações parciais, caso 01.

Aula 15  (02/07/25) Casos 2 e 3 da decomposição em frações parciais.

Aula 16 (04/07/25) Caso 4 de decomposição em frações parciais.

Aula 17  (09/07/25) Exercício sobre decomposição em frações parciais. Integrais trigonométricas via troca universal.

 

 

𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰𒒰

Funções Transcendentes (Matemática Noturno)

Nesta disciplina estudaremos as funções exponenciais, logarítmicas, trigonométricas diretas e inversas, funções extremamente importantes no Cálculo e na Matemática em geral.

Plano de ensino

Uma cópia em pdf do plano de ensino pode ser baixada clicando aqui.

 

Datas das provas

Prova 01: dia 25/06/25 – Gabarito

Prova 02: dia 20/08/25

Exame: dia 27/08/25

 

Listas de Exercícios

• Lista 01 – Exponenciais e logaritmos.
• Lista 02 – Trigonometria no triângulo retângulo. Arcos e ângulos. Ciclo trigonométrico.
• Lista 03 – Números trigonométricos.
• Lista 04 – Fórmulas da Trigonometria. Triângulo quaisquer.

 

Extras

• zero elevado à zero, quanto é? Vídeo do IMPA. Acesso aqui.
• Resoluções de questões da Lista 01, acesso aqui
• Resoluções de exercícios da Lista 02, acesso aqui
• Resoluções de exercícios da Lista 03, acesso aqui

Arquivos pdf das aulas

Aula 01 (30/04/25) Apresentação da disciplina. Função exponencial. Conceito e propriedade de crescimento e de crescimento. Gráficos. Equação exponencial.

Aula 02 (07/05/25) equação e inequação exponencial. Logaritmos. Definição e exemplos. Propriedades dos logaritmos.

Aula 03  (14/05/25) Mudança de base de logaritmos. Equação logarítmica. Inequação logarítmica. Função logarítmica.

Aula 04  (21/05/25) Meia-vida de material radioativo. Injetividade, sobrejetividade e bijetividade de funções.  Funções inversas. As funções exponencial e logarítmica como inversas uma da outra.

Aula 05  (28/05/25) Trigonometria, primeiros conceitos. Arcos e ângulos. Trigonometria no triângulo retângulo.

Aula 06 (04/06/25) Ciclo trigonométrico. Arcos no ciclo. Arcos côngruos, expressão geral e menor determinação. Seno, cosseno e tangente no ciclo.  Arcos notáveis.

Aula 07  (11/06/25) Redução ao primeiro quadrante. Cotangente, secante e cossecante no ciclo trigonométrico. Fórmulas envolvendo esses números trigonométricos. Redução ao primeiro quadrante destes.

Aula 08 (18/06/25) seno e cosseno da adição e subtração de arcos. Resolução de exercícios das listas 02 e 03.

Aula 09  (02/07/25) Formulas da trigonometria, de arcos duplos, arcos metade e da prostaferese.

Aula 10  (09/07/25) Triângulos quaisquer, A função seno.