Resumo da epidemia:
- no mundo: Casos confirmados: 1.911.000; Total de óbitos: 119.000; Total de recuperados: 448.000
- no Brasil: Casos confirmados: 23.430; Total de óbitos: 1.328
- no RS: Casos confirmados: 664; Total de óbitos: 16
- em Porto Alegre / RS: Casos confirmados: 315; Total de óbitos: 7
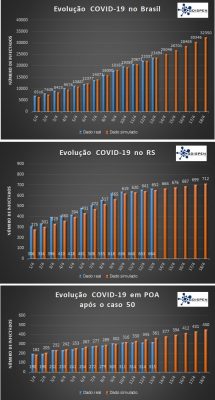
Na atualização de hoje apresentam-se três gráficos da evolução do COVID-19: para o Brasil, Rio Grande do Sul e Porto Alegre. As predições foram calculadas a partir do número atualizado de casos confirmados. A tendência estimada pode ser alterada conforme as ações implementadas. Devido a subnotificação, realização de poucos testes, bem como um feriado prolongado, observa-se uma modificação na tendência em todas as curvas apresentadas na última atualização de dados (no dia 09.04):
- Para o Brasil, dentro de 5 dias este número chegará a aproximadamente 32.300 infectados.
- Para o RS, dentro de 5 dias este número chegará a aproximadamente 700 infectados.
- Para a capital do RS, POA, dentro de 5 dias este número passará de 450 infectados.
ANÁLISE DE UM PERÍODO DE DISTANCIAMENTO SOCIAL DE 30, 60 e 90 DIAS, E A SUA INFLUÊNCIA CONSIDERANDO 25 E 50% DA POPULAÇÃO
Conforme a epidemia progrediu, muitos países ao redor do mundo implementaram procedimentos de isolamento/distanciamento social para tentar conter a propagação do vírus. No nosso Estado estamos em isolamento/distanciamento social a aproximadamente 30 dias (escolas, universidades, parte do comércio).
Na sequência apresenta-se uma simulação, para uma cidade hipotética com 100.000 habitantes, onde a sua população decide entrar em distanciamento social. Esta simulação não tem o objetivo de servir como base para decisões governamentais em qualquer instância, servindo apenas como um objeto de estudo científico e para demonstrar o achatamento das curvas.
No modelo epidemiológico SIR utilizou-se uma taxa básica de reprodução da doença R0 de 2.6, e período de infecção de 5.2 dias.
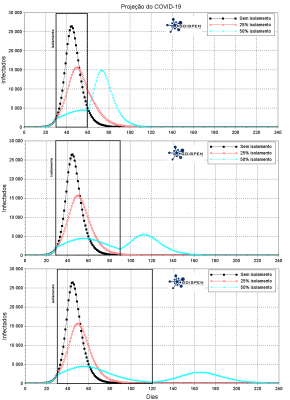
Sem procedimentos de distanciamento social, o pico de infectados acontece em torno de 45 dias depois do início da epidemia, atingindo aproximadamente 27% da população.
Considerando um distanciamento social de 30 dias após a confirmação dos primeiros casos de infecção (iniciando 30 dias a partir do caso 50 confirmado, tendo em torno de 2,5% de infectados):
- Supondo um cenário em que um quarto da população (25%) fique em distanciamento social. Desta forma o pico de infectados acontece em torno de 50 dias depois do início da epidemia, 5 dias depois do caso sem distanciamento social, atingindo aproximadamente 16% da população no pico da epidemia, e um decréscimo contínuo da epidemia na sequência.
- Supondo um cenário em que metade da população (50%) fique em distanciamento social. Com o início do distanciamento social, o número de infectados cresce lentamente, atingindo em torno de 4% da população. Após o término do distanciamento social, o número de infectados cresce, atingindo um novo pico em torno de 15 dias, e tem-se aproximadamente 15% da população infectada (1% a menos do que no pico para o distanciamento social de 25% da população, mas 25 dias depois).
Considerando um distanciamento social de 60 dias:
- 25% da população: Não se observa diferenças significativas em relação ao caso de 30 dias de distanciamento social.
- 50% da população: Com o início do distanciamento social, o número de infectados cresce lentamente, atingindo 4% da população pessoas em torno de 25 dias e depois tem-se um decréscimo até aproximadamente o valor de infectados do início do distanciamento social. Após o término do distanciamento social, o número de infectados cresce novamente e atinge um pico em torno de 22 dias tendo pouco mais de 5% de infectados (3 vezes menor do que no caso de 30 dias de distanciamento social).
Considerando um distanciamento social de 90 dias:
- 25% da população: Não se observa diferenças significativas em relação ao caso de 30 dias de distanciamento social.
- 50% da população: Temos que durante o distanciamento social a epidemia decai quase que totalmente, tendo um pequeno pico de infectados após o retorno, de aproximadamente 2,5% da população, em torno de 45 dias após o fim do distanciamento social (metade da população em relação ao distanciamento social de 60 dias).
Comparando os 3 cenários, percebe-se o achatamento das curvas devido ao tempo de distanciamento social. Nota-se que quando se tem 50% da população em distanciamento social, a curva dos infectados não cresce muito e pode-se manter o pico a valores relativamente baixos, desde que mantenha-se esse distanciamento por um período superior a 60 ou 90 dias.
Detalhes desta pesquisa são encontradas no site do laboratório GDISPEN (https://wp.ufpel.edu.br/fentransporte/), no Facebook do mestrado em Modelagem Matemática da UFPel (https://www.facebook.com/modelagemmatematica.ufpel.1) e no Instagram (@ppgmmat).
Responsáveis: Daniela Buske, Glênio Aguiar Gonçalves e Régis Sperotto de Quadros
Laboratório GDISPEN (Grupo de Dispersão de Poluentes & Engenharia Nuclear), Programa de Pós-Graduação em Modelagem Matemática (PPGMMat), Universidade Federal de Pelotas (UFPel).