Os pesquisadores do GDISPEN publicaram hoje um resumo da pesquisa, explicando rapidamente o modelo utilizado na obtenção dos dados desta pesquisa (https://wp.ufpel.edu.br/fentransporte/2020/04/09/a-evolucao-epide…id-19-modelo-sir/ ). Este documento será constantemente atualizado e modificado.
Resumo da epidemia no mundo: Dados confirmados: 1.587.000; Total de óbitos: 95.000; Total de recuperados: 353.000
Resumo da epidemia no Brasil: Dados confirmados: 17.857; Total de óbitos: 941
Resumo da epidemia no RS: Dados confirmados: 618; Total de óbitos: 12
Resumo da epidemia em Porto Alegre / RS: Dados confirmados: 303; Total de óbitos: 6
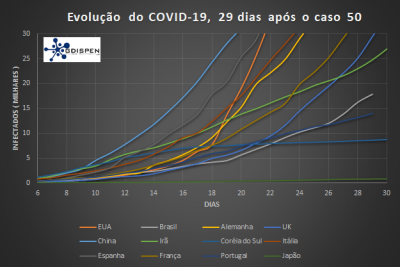
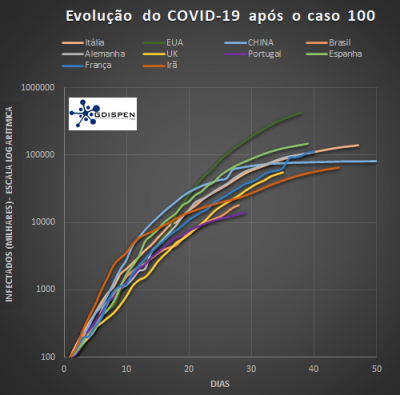
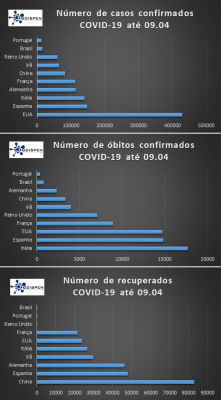
Nos primeiros três gráficos temos os dados reais da epidemia para os países com o maior número de infectados, incluindo o Brasil. No primeiro gráfico podemos ver a evolução da epidemia após o caso 50 confirmado. No momento o Brasil segue a inclinação da curva do Reino Unido, e ultrapassou a curva de crescimento de Portugal. No segundo gráfico vemos a evolução a partir do caso 100 confirmado, em escala logarítmica. No terceiro gráfico temos a evolução dos casos confirmados, óbitos e recuperados, em ordem crescente de casos em cada categoria.
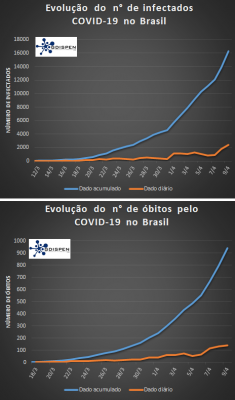
Na quarta figura apresentam-se os gráficos da evolução da epidemia no Brasil, tanto para o número de infectados quanto para o de óbitos. Inseriu-se no gráfico os valores totais e diários.
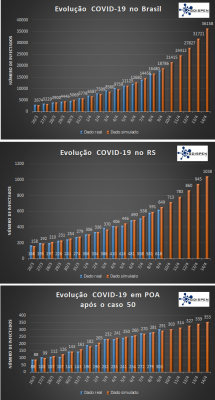
Na última figura temos três gráficos da evolução do COVID-19: para o Brasil, Rio Grande do Sul e Porto Alegre. As predições foram calculadas a partir dos dados confirmados atualizados. A tendência estimada pode ser alterada conforme as ações implementadas.
- Para o Brasil, dentro de 5 dias este número chegará a aproximadamente 36.000 infectados.
- Para o RS, dentro de 5 dias este número chegará a aproximadamente 1000 infectados.
- Para a capital do RS, POA, dentro de 5 dias este número passará de 350 infectados. A tendência da curva se modificou nos últimos dias.
Detalhes da pesquisa no site do laboratório GDISPEN (https://wp.ufpel.edu.br/fentransporte/) e no Facebook do mestrado em Modelagem Matemática da UFPel (https://www.facebook.com/modelagemmatematica.ufpel.1).
Responsáveis: Daniela Buske, Glênio Aguiar Gonçalves e Régis Sperotto de Quadros
Laboratório GDISPEN (Grupo de Dispersão de Poluentes & Engenharia Nuclear), Programa de Pós-Graduação em Modelagem Matemática (PPGMMat), Universidade Federal de Pelotas (UFPel).