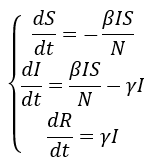abr 09

A evolução epidêmica do COVID-19 – Modelo SIR

Este documento tem por objetivo explicar o modelo e os parâmetros utilizados pelos pesquisadores do GDISPEN para a modelagem matemática do COVID-19. O documento será constantemente atualizado e incrementado. A pesquisa “A EVOLUÇÃO EPIDÊMICA DO COVID-19 – MODELO SIR” está sob a responsabilidade dos doutores Daniela Buske,  Glênio Aguiar Gonçalves e Régis Sperotto de Quadros, do Laboratório do Grupo de Dispersão de Poluentes & Engenharia Nuclear (GDISPEN). Os pesquisadores do GDISPEN são docentes do DME / IFM / PPGMMat  / UFPel– Pelotas / RS / Brasil.

Este estudo tem finalidade puramente acadêmica e científica, mostrando a grande aplicabilidade da modelagem matemática em problemas reais. As discussões, opiniões, idéias e publicações geradas a partir dos resultados do modelo utilizado são de autoria dos respectivos autores, e não necessariamente representam aquelas das instituições a que estes pertencem.

Os pesquisadores utilizaram inicialmente o modelo epidemiológico SIR (Suscetível-Infectado-Recuperado) (McKendrick e Kermack, 1927, 1932, 1933, republicados em 1991). Este modelo simples, porém, considerado robusto para modelar epidemias como o COVID-19, é bem conhecido na literatura e mostra a evolução de uma população suscetível S, infectada I e recuperada R. O modelo SIR tem sido amplamente utilizado para modelar o COVID-19. O conjunto de equações mais simples do modelo SIR é dada por:

onde β e γ são positivos, sendo β a taxa de infecção e γ  a taxa de recuperação dos indivíduos, e N = S + I + R é o total da população. O código computacional foi desenvolvido em linguagem SCILAB.

  • Suscetíveis: indivíduos ainda não expostos e que podem adquirir a infecção.
  • Infectados: indivíduos infectados, doentes ou não, que podem transmitir para outras pessoas.
  • Recuperados/Removidos: indivíduos que se infectaram e se recuperaram, adquirindo imunidade; ou os que morreram em decorrência da doença.

Um modelo matemático se apoia em premissas e hipóteses sobre o fenômeno estudado, no qual são inseridas informações de parâmetros. Inicialmente os parâmetros são estimados com base no conhecimento acumulado em epidemias anteriores ou, da própria epidemia e do seu desenvolvimento em outros locais. No decorrer da epidemia os parâmetros vão sendo melhor definidos e os modelos tornam-se mais robustos, uma vez que o conhecimento e a característica da epidemia ficam mais claros.

No modelo SIR temos dois parâmetros importantes: a taxa de transmissão β (para quantas pessoas, em média, um indivíduo infectado pode transmitir a doença) e a taxa de recuperação γ. Neste modelo, considera-se que indivíduos já infectados não podem ser infectados novamente.

Medidas de distanciamento social e de conscientização da população acerca dos sintomas do Covid-19 aumentam as chances de que as pessoas permaneçam em suas casas, reduzindo a exposição, independente de terem sintomas. Também aumentam as chances de que pessoas com sintomas respiratórios evitem transitar nas ruas, mantendo-se em auto quarentena, evitando a transmissão para outras pessoas. Uma observação importante é que as medidas de isolamento ou restrições não são observadas imediatamente no número de casos, pois existe uma defasagem entre o momento da infecção e o aparecimento de sintomas (período de incubação). O tempo de incubação do COVID-19 é de 5 a 14 dias (tendo referências que citam 5 a 18 e 5 a 21 dias).

Na literatura encontram-se três cenários, considerando um período distinto em que indivíduos infectados se mantêm em circulação, podendo transmitir o vírus para pessoas suscetíveis, em função das medidas de distanciamento social: 5, 14 e 21 dias. Resultados apontam que as medidas de distanciamento social têm como consequência não apenas a diminuição do número total de casos, mas, principalmente, do número de casos ativos. Isto diminui a pressão sobre os serviços de saúde e é conhecido como fenômeno de “achatamento da curva”.

Nas simulações da expansão da Epidemia no Brasil, considerou-se um período de infecção de 5.2 dias (taxa de recuperação γ = 1/5.2), uma vez que restrições quanto à circulação, como fechamento de universidades e escolas iniciaram a ser tomadas em torno do dia 16 de março em diversos Estados.

A reprodutibilidade basal é medida pelo parâmetro R0 (taxa de reprodução) e significa o número médio de pessoas que são infectadas por um único indivíduo, R0=β/γ. Segundo publicação recente do Imperial College e de outras fontes da literatura, este valor varia entre 2 e 4 (2.6 a 3.5), no caso do COVID-19. Este valor se modifica ao longo do desenvolvimento da epidemia. Se R0 < 1, então o número de infectados será decrescente e a epidemia se erradicará. No caso em que R0 > 1 a epidemia persistirá na população. Conhecendo R0 e γ podemos encontrar a taxa de infecção β.

  • Para o Brasil considerou-se R1 = 3.2 até 8 dias depois do caso 50, R2=2.08 de 9 a 18 dias, R3 = 1.72 de 19 a 30 dias e R4 = 1.4 para o restante dos dias.
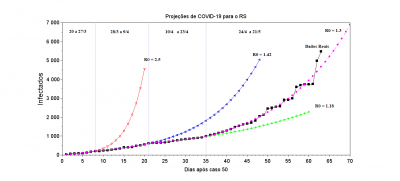
  • Para o RS considerou-se R1= 2.5 até 8 dias depois do caso 50, R2=1.42 de 9 a 21 dias, R3 = 1.18 de 22 a 35 dias e R4 = 1.30 para o restante dos dias (no gráfico temos um exemplo de como seria o crescimento da curva, se fosse mantido o R0 de cada período)
  • Para Porto Alegre considerou-se R1= 1.67 até 9 dias depois do caso 50, R2=1.17 de 10 a 23 dias, R3 = 1.08 para o restante dos dias.

Os dados confirmados da epidemia são disponibilizados online. Neste trabalho são utilizados os dados disponibilizados pela Universidade John Hopkins (EUA), pela Organização Mundial de Saúde (OMS), secretarias estaduais, a Wikipedia e Ministério da Saúde do Brasil. Os dados confirmados da epidemia são comparados com o modelo matemático SIR.

Em uma entrevista para a rede americana CNN no dia 29 de março, o infectologista Anthony Fauci, um dos mais respeitados do mundo, declarou que a pandemia é um “alvo em movimento”. Assim, pequenas mudanças nos números divulgados pelas autoridades, ou nos parâmetros utilizados no modelo epidemiológico, irão causar grandes variações no número de infectados no futuro. Lembrando que a tendência estimada da curva pode ser alterada conforme as ações implementadas pelo governo.

*arquivo atualizado em 22.05.2020

Referências bibliográficas:

Adam, D., 2020. Special report: The simulations driving the world’s response to COVID-19, How epidemiologists rushed to model the coronavirus pandemic. Nature 580, 316-318. DOI: 10.1038/d41586-020-01003-6

Anastassopoulou, C. Russo, L., Tsakris, A., Siettos, C., 2020. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. Plos One. DOI: 10.1371/journal.pone.0230405

Dong, E., Du, H., Gardner, L., 2020. An interactive web-based dashboard to track COVID-19 in real time. The Lancet Infectious Diseases. DOI: 10.1016/S1473-3099(20)30120-1

Hethcote, H. W., 2000. The Mathematics of Infectious Diseases. SIAM Review 42, 599–653.

Imai, N., Cori, A., Dorigatti, I., Baguelin, M., Donnelly, C.A., Riley, S., 2020. Report 3: transmissibility of 2019-nCoV. British Medical Journal Publishing Group.

Jia, J., Hu, X., Yang, F., Song, X., Dong, L., Zhang, J., Jiang, F., Gao, R., 2020. Epidemiological Characteristics on the Clustering Nature of COVID-19 in Qingdao City, 2020: A Descriptive Analysis. Society for Disaster Medicine and Public Health Preparedness. DOI: 10.1017/dmp.2020.59

Kermack, W., McKendrick, A., 1991. Contributions to the mathematical theory of epidemics-I. 1927.  Bulletin of Mathematical Biology 53 (1-2), 33-55. DOI:10.1007/BF02464423.

Kermack, W., McKendrick, A., 1991. Contributions to the mathematical theory of epidemics-II. The problem of endemicity. Bulletin of Mathematical Biology 53 (1-2), 57-87. DOI :10.1007/BF02464424.

Kermack, W., McKendrick, A., 1991. Contributions to the mathematical theory of epidemics-III. Further studies of the problem of endemicity. Bulletin of Mathematical Biology 53 (1-2), 89-118. DOI:10.1007/BF02464425.

Kissler, S.M., Tedijanto, C., Goldstein, E., Grad, Y.H., Lipsitch, M., 2020, Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period, Science DOI: 10.1126/science.abb5793.

Kucharski, A.J., Russel, T.W., Diamond, C., Liu, Y., Edmunds, J., Funk, S., Eggo, R.M., 2020. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. The Lancet Infectious Diseases. DOI:10.1016/ S1473-3099(20)30144-4

Lauer, S.A., Grantz, K.H., Bi, Q., Jones, F.K., Zheng, Q.; Meredith, H.R., Azman, A.S., Reich, N.G., Lessler, J., 2020. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Annals of Internal Medicine. DOI: 10.7326/M20-0504

Li, R., Pei, S., Chen, B., Song, Y., Zhang, T., Yang, W., Shaman, J., 2020. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2). Science. DOI: 10.1126/science.abb3221

Lin, Q., Zhao, S., Gao, D., Lou, Y., Yang, S., Musa, S.S., Wang, M.H., Weiming Wang, Y.C., Yang, L., He, D. (2020). A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. International Journal of Infectious Diseases 93, 211–216. DOI: 10.1016/j.ijid.2020.02.058

Linton, N.M., Kobayashi,T., Yang, Y., Hayashi, K., Akhmetzhanov, A.R., Jung, S., Yuan, B., Kinoshita, R., Nishiura, H., 2020. Epidemiological characteristics of novel coronavirus infection: A statistical analysis of publicly available case data. medRxiv preprint doi: DOI: 10.1101/2020.01.26.20018754.

Liu, Y., Gavle, A.A., Wilder-Smith, A., Rocklöv, J., 2020. The reproductive number of COVID-19 is higher compared to SARS coronavirus. Journal of Travel Medicine 27 (2), DOI: 10.1093/jtm/taaa021

Moss, R., Wood, J., Brown, D., Shearer, F., Black, A.J., Cheng, A.C., McCaw, J.M., McVernon, J., Modelling the impact of COVID-19 in Australia to inform transmission reducing measures and health system preparedness. MedRxiv preprint DOI: 10.1101/2020.04.07.20056184.

Piazza, F., Fanelli, D., 2020. Analysis and forecast of COVID-19 spreading. https://www.researchgate.net/project/Analysis-and-forecast-of-COVID-19-spreading

Prem, K., Liu, Y., Russell, T.W., Kucharski, A.J., Eggo, R.M., Davies, N., 2020. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. The Lancet Infectious Diseases. DOI:10.1016/S2468-2667(20)30073-6

Riou, J., Althaus, C.L., 2020. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), Eurosurveillance 25(4).

Sanche, S., Lin, Y.T., Xu, C., Romero-Severson, E., Hengartner, N., Ke, R., 2020. High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2. Emerging Infectious Diseases. DOI: 10.3201/eid2607.200282

She, J., Liu, L., Liu, W., 2020. COVID-19 epidemic: Disease characteristics in children. Journal of Medical Virology. DOI: 10.1002/jmv.25807

Tian, S., Hu, N., Lou, J., Chen, K., Kang, X., Xiang, Z., Chen, H., Wang, D., Liu, N., Chen, G., Zhang, Y., Li, D., Li, J., Lian, H., Niu, S., Zhang, L., Zhang, J., 2020. Characteristics of COVID-19 infection in Beijing. Journal of Infection 80, 401-406. DOI: 10.1016/j.jinf.2020.02.018

Tuite, A.R., Fismann, D.N., Greer, A.L., 2020. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ. DOI: 10.1503/cmaj.200606

Walker, P.G.T., Whitaker, C., Watson, O., et al., 2020. Report 12: The global impact of COVID-19 and strategies for mitigation and suppression. https://www.imperial.ac.uk/media/imperial-college/medicine/mrc-gida/2020-03-26-COVID19-Report-12.pdf

Wang, H., Wang, Z., Dong, Y., Chang, R., Xu, C., Zhang, S., Tsamlag, L., Shang, M., Huang, J., Wang, Y., Xu, G., Shen, T., Zhang, X., Cai, Y., 2020. Phase-adjusted estimation of the number of Coronavirus Disease 2019 cases in Wuhan, China. Cell Discovery 6. https://www.nature.com/articles/s41421-020-0148-0

World Health Organization, Coronavirus disease (COVID-2019) situation reports.

Wu, J.T., Leung, K., Leung, G.M., 2020. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. The Lancet Infectious Diseases. DOI:10.1016/ S0140-6736(20)30260-9

Ye, Y., Lagniton, P.N.P., Ye, S., Li, E., Xu,R., 2020. COVID-19: whats has been learned and to be learned novel coronavirus disease. International Journal of Biological Science 16 (10), 1753-1766. DOI:10.7150/ijbs.45134

Zhao, S., Lin, Q., Ran, J., Musa, S.S., Yang, G., Wang, W., Lou, Y., Gao, D., Yang, L., He, D., Wang, M.H., 2020. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. International Journal of Infectious Diseases 92, 214-217. DOI: 10.1016/j.ijid.2020.01.050

Zhao, S., Musa, S.S., Lin, Q., Ran, J., Yang, G., Wang, W., Lou, Y., Yang, L., Gao, D., He, D., Wang, M., 2020. Estimating the unreported number of novel Coronavirus (2019-nCoV) cases in China in the first half of January 2020: a data-driven modelling analysis of the early outbreak. Journal of Clinical Medicine 9(2). DOI:10.3390/jcm9020388

 

Sites utilizados para visualização de dados e acompanhamento da epidemia:

 

fentransporte