Nível: Ensino Médio
Noções a serem exploradas: Distância Euclidiana no plano, sistemas de coordenadas no plano.
Participantes: 2 jogadores por tabuleiro. Haverá quatro tabuleiros e dois monitores.
Objetivo: chegar o mais próximo possível do território do adversário;
Materiais: quatro tabuleiros 7 x 7 com os territórios de cada jogador fixados em extremos opostos no tabuleiro, conforme a figura; algumas células do tabuleiro são destacadas, pintadas de outra cor; dois objetos representando Pokémons e que aqui serão chamados de pinos; dois dados de cores distintas com seis faces, um deles representará o movimento para a direita e o outro para a frente; dez cartas com perguntas relacionadas a localização no plano; dez cartas com um Pokémon e poder de luta pré-fixado, régua de apoio.
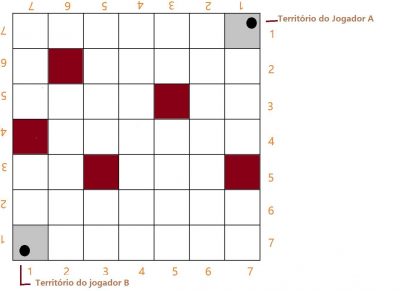
Figura 14
Cenário: Inicia-se a partida com o pino de cada jogador sendo posicionado em seu território conforme a figura 14.
Como jogar? O jogador mais novo irá jogar os dois dados simultaneamente. Irá mover o pino sobre o tabuleiro segundo os números que saíram nos dados. Por exemplo: se saiu o número 3 no dado de cor verde e 4 no dado de cor amarelo, o pino será deslocado três unidades na horizontal para a direita e quatro na vertical para frente. Em seguida, será a vez do próximo jogador, e assim por diante. Ao serem sorteados nos dados números que ultrapassariam as casas do tabuleiro, o pino deve ser deslocado em sentidos opostos, ou seja, horizontal para a esquerda e vertical para baixo. Caso a posição ao final da jogada seja sobre uma célula destacada, o jogador deverá sortear uma carta e responder corretamente à pergunta feita nesta carta. Neste caso poderá lançar os dados novamente. Caso não acerte a pergunta, será a vez de seu adversário lançar os dados. Caso os pinos dos dois jogadores fiquem posicionados na mesma cédula, cada um sorteará uma das cartas com o Pokémon e o poder de luta. O que estiver com o Pokémon com poder de luta maior terá direito a mover uma casa na diagonal na direção do território de ser adversário. A ordem de arremesso de dados não será alterada. O jogo termina quando um pino chega no território do adversário ou depois de transcorridos 5 minutos de jogo. Neste último caso, o ganhador será o jogador que estiver mais próximo do território do adversário.
Resolução da atividade: depende de cada jogada.
Durante a execução da atividade, o monitor irá fazer perguntas instigadoras aos dois jogadores, estimulando a noção de localização, por exemplo:
-
O que significa, no tabuleiro, ficar mais próximo do território do adversário? Espera-se aqui que o jogador (estudante do Ensino Médio) saiba calcular a distância a partir da contagem das células na horizontal e na vertical, aplicando o teorema de Pitágoras
-
É possível este jogo dar empate?
Uma variação do jogo pode ter um tabuleiro envolvendo para coordenadas também números negativos;
As cartas terão as seguintes perguntas:
-
Quais são as coordenadas da célula que você se encontra com relação ao seu território?
-
Quais são as coordenadas da célula que você se encontra com relação ao território do seu adversário?
-
A distância da célula que você se encontra com relação ao seu território é maior ou menor do que as somas das coordenadas de sua posição?
-
Qual a distância que se encontra o seu pino e de seu adversário?
-
Quais as coordenadas do território inicial?
-
Quais as coordenadas do território inicial de seu adversário?
-
Qual é a distância entre os territórios?
-
Quais as coordenadas da célula que está no centro do tabuleiro? Por que?
-
Qual é a célula simétrica, em relação ao centro do tabuleiro, à que você se encontra?
-
Qual a figura geométrica formada pelo segmento que une a célula que você se encontra ao seu território e um dos lados do tabuleiro?
No decorrer de todas as atividades, os monitores farão perguntas aos jogadores, de acordo com sua faixa etária, procurando estimulá-los a explicitarem oralmente seu raciocínio. As respostas não serão fornecidas sem que o participante pense a respeito.