Embora as funções financeiras não sejam tão complexas, deixamos para a última parte deste curso por entendermos que se trata de uso muito mais especializado das funções das Planilhas do Google, nesta seção exploraremos brevemente as principais funções da área financeira, voltadas a cálculos de Taxas, Valor Futuro, Lucros, Depreciação e etc.
VALOR FUTURO – Capitalização
O Valor futuro refere-se à capitalização de um bem financeiro qualquer. O investimento pode ser um imóvel, ações, cotas em um fundo, etc. Se você optasse por deixar R$100 embaixo do colchão ao passo que eu deposito R$100 em uma conta bancária que pagará juros sobre tal depósito, quem terá mais poder aquisitivo dentro de 10 anos? A pergunta pode parecer simples, mas é através dela que podemos compreender o valor do dinheiro no tempo. Conforme o tempo passa, se não houver correção, o dinheiro perde valor, embora o valor de face permaneça o mesmo.
Ao calcularmos o valor futuro de um investimento estamos interessados em saber o quanto ele valerá no futuro. Esta é uma forma de planejamento, pois através deste conhecimento podemos tomar decisões sobre o consumo agora e o consumo no futuro. Se você sabe que o carro de seus sonhos custa R$33 mil e a taxa paga pelo seu banco sobre um depósito é de 10% a.a, se o valor do automóvel continua o mesmo pelos próximos doze meses, talvez seja mais interessante depositar R$30 mil, hoje, e comprar o carro no final do ano. Através do adiamento do consumo você economizará R$3 mil, pois os R$33 mil valem apenas R$30 mil.
Obviamente que a decisão também depende da importância de se ter o carro agora. Mas a decisão final certamente ficará mais clara quanto você reconhecer o real valor do automóvel em relação a sua real necessidade. Se a necessidade não é imediata é interessante adiar o consumo. Se por outro lado a compra do carro gerará um retorno, pois você o utiliza para trabalhar e ganhar dinheiro; então, será interessante comprar o carro agora. Contudo, pontos subjetivos de sua decisão final ficarão muito mais objetivos com tais ferramentas em mãos. Na planilha, para avaliarmos o valor futuro utilizamos a função VF. Esta função avalia o valor futuro de um pagamento único, uma série de pagamentos ou a combinação dos dois.
Função VF
A fórmula é dada como VF (taxa, numero_de_periodos, valor_do_pagamento, valor_atual, [fim_ou_inicio]) onde:
- taxa é a taxa de juros por período;
- numero_de_periodos: o número de pagamentos a serem feitos.
- valor_do_pagamento: o valor por período a ser pago.
- valor_atual: o valor atual da anuidade.
- fim_ou_inicio: [ OPCIONAL – 0 por padrão ] – indica se os pagamentos são feitos no final (0) ou no início (1) de cada período.
Exemplos:
Iniciaremos com exemplos de pagamento únicos, passando por uma série de pagamentos e finalmente a combinação dos dois. Abaixo desenvolvemos várias questões envolvendo valores futuros.
1. Você efetua um investimento de R$1.000 para resgatar em cinco anos. Se a taxa anual nominal é de 15% e os juros são capitalizados mensalmente, qual será o valor do resgate daqui a cinco anos?
=VF(15%/12;12*5;0;-1000;0)
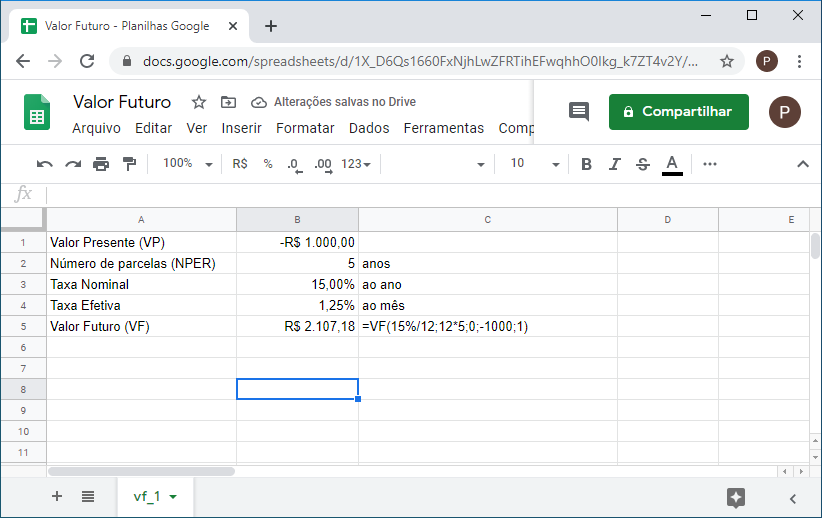
2. Efetuando o cálculo anterior para pagamento no início do investimento, temos:
=VF(15%/12;12*5;0;-1000;1)
Para pagamento único não fará diferença no cálculo final.
3. Você faz um investimento que paga 0,055% ao dia de juros. Se o investimento for resgatado em um ano, quanto você terá recebido por um investimento inicial de R$3.000? Considere um ano de 252 dias úteis.
Considerando que a taxa é cotada como sendo diária, não há necessidade de proporcioná-la, portanto o valor futuro é:
=VF(0,00055;252;0;-3000;0)
Resultando 3.445,86
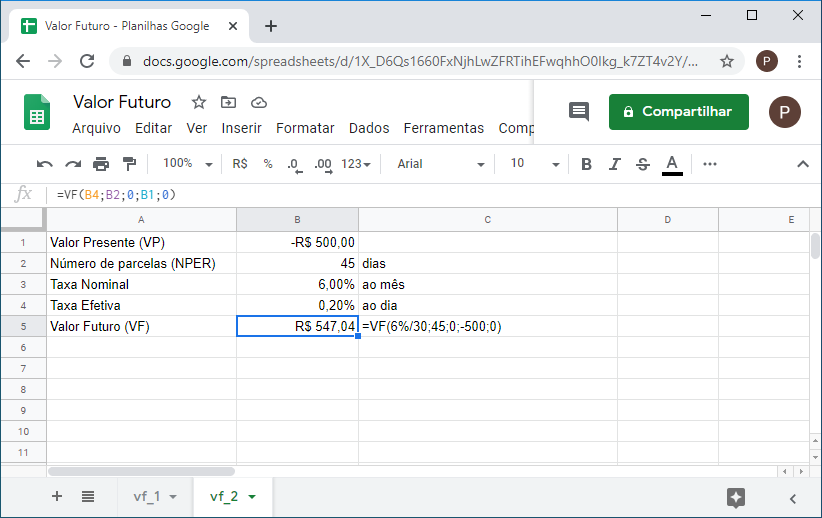
4. Sabendo que a taxa cobrada para um empréstimo é 6% ao mês, se o empréstimo for pago após 45 dias, qual o valor a ser pago, se a retirada foi de R$500,00 e os juros aplicados diariamente?
Neste exemplo, vamos considerar um mês de 30 dias. Portanto a taxa deve ser proporcionada por 30.
=VF(6%/30;45;0;-500;0)
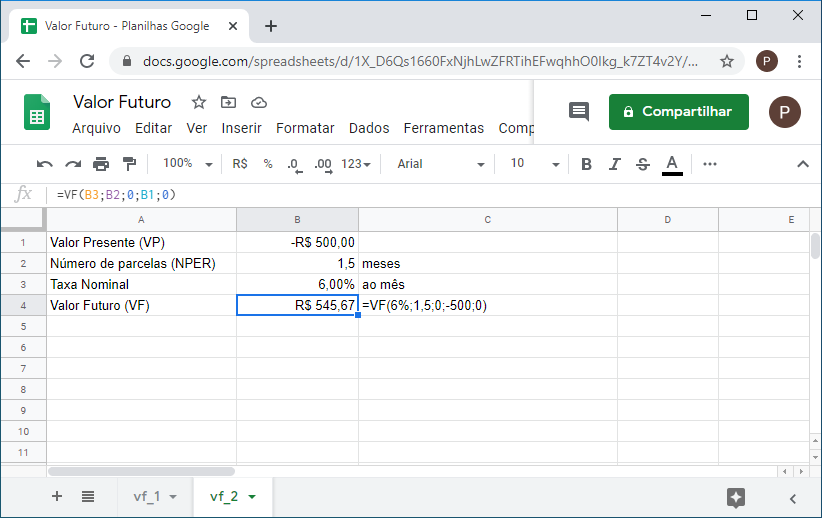
5. Utilizando o mesmo exemplo anterior, qual será o valor futuro se a capitalização é mensal? Com a capitalização mensal nós precisamos observar que no primeiro mês a capitalização é total, isto é, os 6% são aplicados sobre os R$500. Porém, para o período seguinte o valor é capitalizado no 15º dia. Portanto, a capitalização não é completa e precisamos calcular a taxa equivalente no período.
=VF(6%;1,5;0;-500;0)
6. Sabendo que a taxa anual nominal é de 77% para empréstimos pessoais, quanto você deverá pagar por um empréstimo de R$1.000 liquidado ao final de seis meses se a capitalização é mensal?
Como a taxa é cotada por ano, precisamos proporcioná-la para o tipo de capitalização. Neste caso a capitalização é mensal, logo o NPER é igual a 6.
=VF(0,77/12;6;0;-1000;0)
Resultando 1.452,31
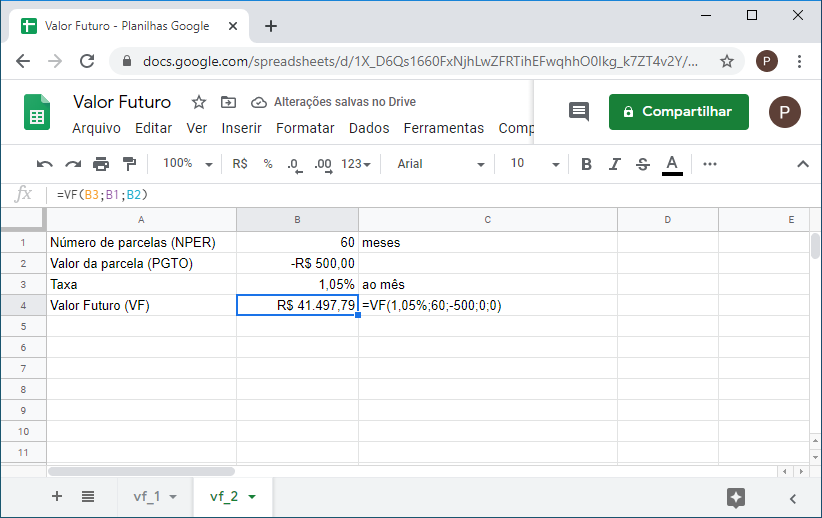
7. Pelos próximos 5 anos você fará um depósito mensal de R$500 em um fundo de investimento. Se a taxa paga pelo fundo é 1,05% ao mês, quanto você terá acumulado neste período?
Diferentemente dos problemas anteriores, aqui, nós não possuímos uma valor presente fixo. Ao invés disso, temos um depósito constante de R$500 por um período de 60 meses. A função continua a mesma, mas os argumentos são entrados de forma diferente:
=VF(1,05%;60;-500;0;0)
8. Recalculando o problema acima para pagamento no início do período.
Como o pagamento ocorre no início do período, há um movimento na regra de “tempo”. No cálculo efetuado na planilha, basta modificar o último parâmetro de “zero” para “um”:
=VF(0,0105;60;-500;0;1)
Resultando R$ 41.933,52
VALOR PRESENTE – Desconto
Valor presente ou valor atual refere-se a uma quantia hoje em dinheiro corrente. Se você vai receber R$100 dentro de um ano, hoje, ele vale menos. Portanto, o valor presente é aquele valor que capitalizado pelo próximo ano gera os R$100,00 no final do ano. Em outras palavras, o valor presente nada mais é do que o inverso do valor futuro. Valores presentes podem ser utilizados para descontar notas promissórias, títulos, cheques, etc.
Se você financiar um bem qualquer em varias parcelas e resolver pagar adiantado algumas parcelas, obviamente que você sairá perdendo a menos que você tenha um desconto sobre o valor total. O desconto mínimo é aquele que fornece um rendimento exatamente igual à diferença descontada. Este é o mínimo requerido para que nem você nem a financeira saiam perdendo nesta transação. A pergunta que você deve estar fazendo é: se nem a financeira nem você sai perdendo, então, porque entrar nessa?
A verdade é que você somente entra por acreditar que não será possível ter o mesmo rendimento dado o desconto. Se você acredita que a taxa de juros vai cair nos próximos meses, então, se você consegue assegurar um desconto maior do que você acredita conseguir de juros no banco, você sairá ganhando. Por outro lado, se a taxa subir e a financeira investir o dinheiro sabiamente, ela sairá ganhando. Mas deixando as estratégias de lado, vamos ver como o estes cálculos são feitos na planilha.
Para calcular o valor presente de um investimento qualquer, utilizamos a função VP. A função VP retorna o resultado oposto da função VF. Para analisar esse comportamento, vamos reverter os cálculos dos exemplos anteriores.
Função VP
A fórmula é dada como VP(taxa; numero_de_periodos; pagamento_por_periodo; [valor_futuro; fim_ou_inicio])onde:
- taxa é a taxa de juros por período;
- numero_de_periodos: o número de pagamentos a serem feitos.
- valor_do_pagamento: o valor por período a ser pago.
- valor_futuro – [ OPCIONAL ] – O valor futuro restante após o pagamento final.
- fim_ou_inicio: [ OPCIONAL – 0 por padrão ] – indica se os pagamentos são feitos no final (0) ou no início (1) de cada período.
1. Você efetua um investimento e resgata após cinco anos a quantia de R$2.107,18. Se a taxa anual nominal é de 15% e os juros são capitalizados mensalmente, qual o valor presente do investimento?
=VP(15%/12;12*5;0;-2107,18;0)
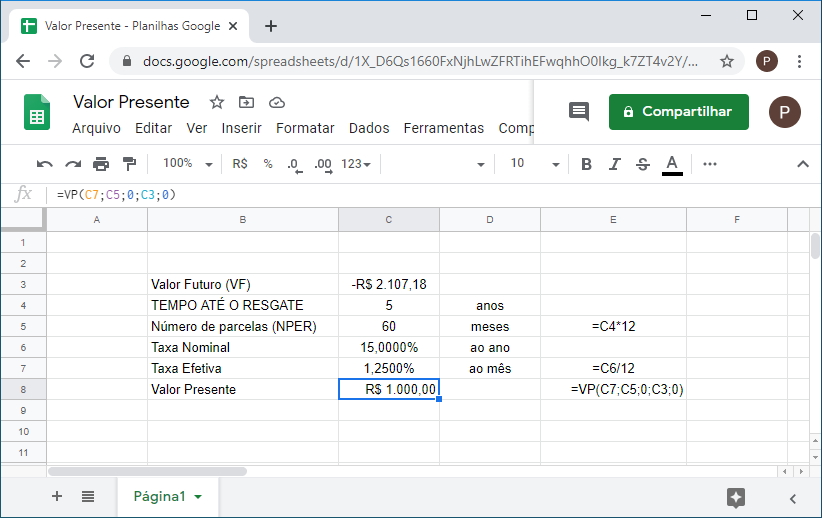
2. Efetuando o cálculo anterior para pagamento no início do investimento.
=VP(15%/12;12*5;0;-2107,18;1) resulta o mesmo valor, portanto, para pagamento único não fará diferença no cálculo final.
3. Você faz um investimento que paga 0,055% ao dia de juros. Se o investimento foi resgatado em um ano, quanto você investiu se o valor resgatado foi de R$3.445,86? Considere um ano de 252 dias úteis.
Considerando que a taxa é cotada como sendo diária, não há necessidade de proporcioná-la, portanto o valor futuro é:
=VP(0,00055;252;0;-3445,86;0)
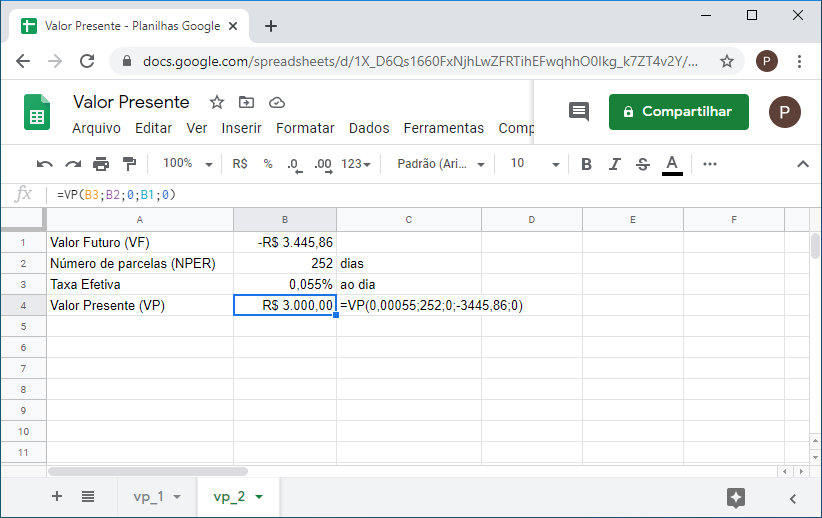
4. Sabendo que a taxa cobrada para um empréstimo é 6% ao mês, e o empréstimo for pago após 45 dias, quanto você pegou emprestado se o valor pago foi de R$547,04 e os juros aplicados diariamente?
Neste exemplo, vamos considerar um mês de 30 dias. Portanto a taxa deve ser proporcionada por 30.
=VP(6%/30;30*1,5;0;-547,04;0) Resultando R$500,00
5. Utilizando o mesmo exemplo anterior, qual será o valor presente se a capitalização é mensal e o valor pago foi de R$545,67?
Como a capitalização é mensal nós precisamos observar que o período de capitalização é de 1,5 meses.
=VP(6%;1,5;0;-545,67;0) Resultando R$500,00
6. Sabendo que a taxa anual nominal é de 77% para empréstimos pessoais, quanto você pegou emprestado se ao final de seis meses você pagou R$1.452,31 com uma capitalização mensal?
Como a taxa é cotada por ano, precisamos proporcioná-la para o tipo de capitalização.
77% / 12, assim temos a taxa mensal.
=VP(77%/12;6;0;-1452,31;0) Resultando R$1.000,00
7. Por 5 anos você fez um depósito mensal que lhe rendeu R$41.497,79 no resgate do fundo de investimento. Se a taxa paga pelo fundo foi de 1,05% ao mês, qual foi o valor depositado mensalmente?
Diferentemente dos problemas anteriores, aqui, nós não possuímos uma valor futuro resultante de um único VP. Ao invés disso, temos vários depósitos mensais constantes por um período de 60 meses. A função usada é:
=PGTO(taxa;NPER;VP;VF;tipo)
=PGTO(1,05%;60;0;41.497,79;0)
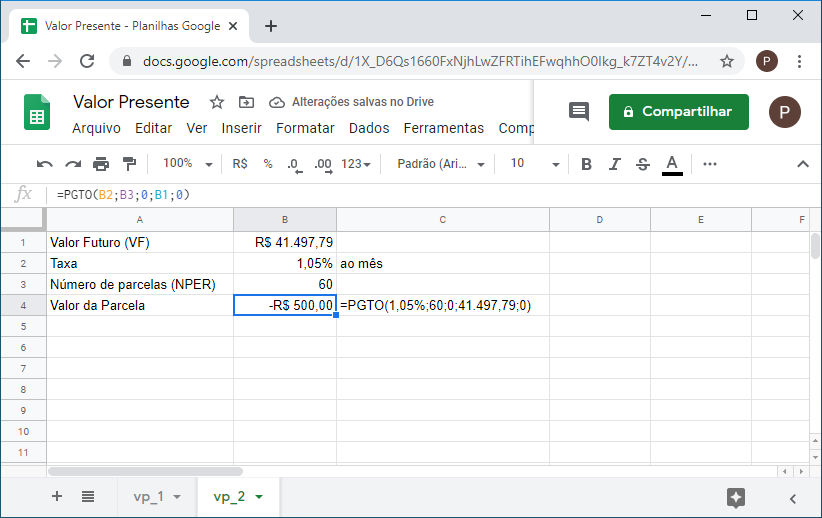
8. Recalcule o problema acima para pagamento no início do período.
Como o pagamento ocorre no início do período, basta modificar o último parâmetro de “zero” para “um”:
=PGTO(1,05%;60;0;41.497,79;1) Resultando R$ 494,80