Período
Como visto até o momento, a partir de certos parâmetros podemos encontrar outros. Às vezes possuímos todos os parâmetros necessários para encontrar o valor presente. Outras vezes, possuímos os parâmetros necessários para encontra o valor futuro ou a taxa de juros aplicada. O que você deve ter notado nos exemplos anteriores é que os argumentos de cada função, na verdade, representam outra função. Por exemplo, na função VP você tem o argumento VF que também é representado pela função VF. Da mesma forma, em ambas as funções têm o argumento TAXA e também possuímos a função TAXA.
Outro argumento preenchido várias vezes é NPER. NPER além de ser um argumento das funções acima, ele também é uma função. A precisão da função NPER dependerá dos valores entrados como argumentos da função. Observe o exemplo abaixo:
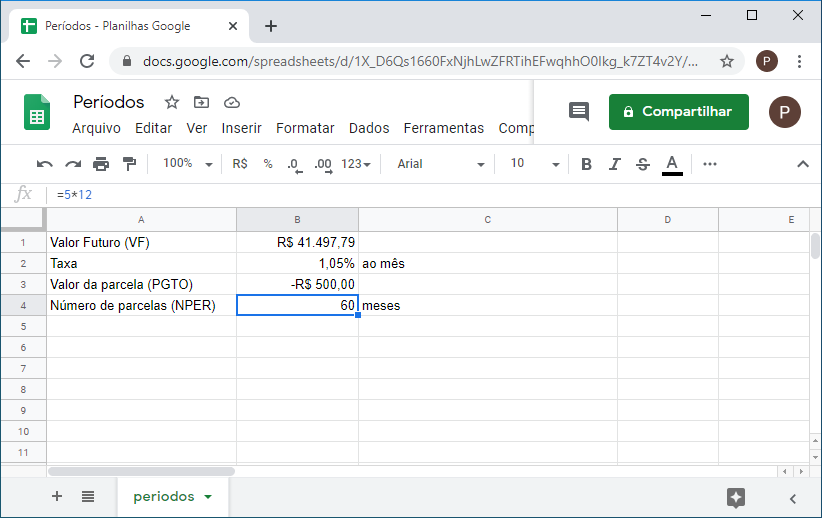
O valor na célula B4 é um valor calculado, portanto o resultado para NPER é exatamente 60 (5*12 utilizado no cálculo do VF).
Este é mais um motivo para você evitar arredondamentos durante o cálculo. Utilize o máximo de precisão possível nos cálculos intermediários e somente faça o arredondamento no final. A seguir apresento exercícios desenvolvidos para fixar a solução do problema:
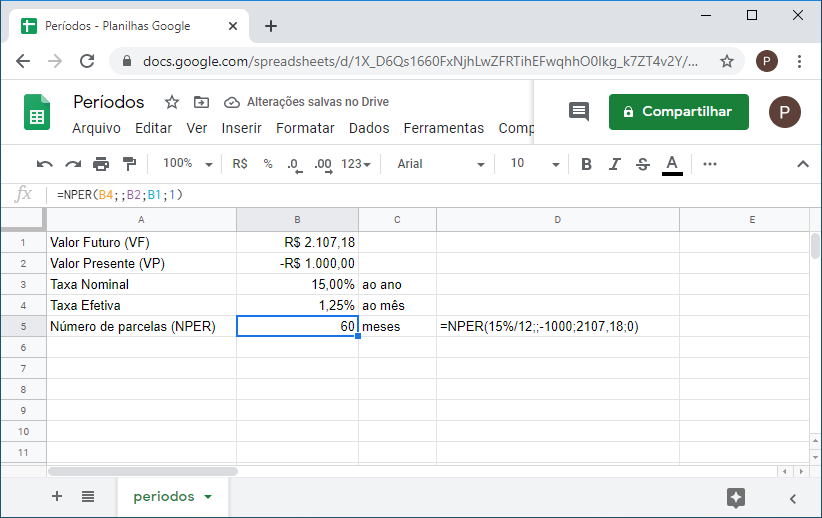
1. Você efetua um investimento de R$1.000 e resgata R$2.107,18. Se a taxa anual nominal é de 15% e os juros são capitalizados mensalmente, quanto tempo durou o investimento?
=NPER(15%/12;;-1000;2107,18;0)
2. Efetue o cálculo anterior para pagamento no início do investimento
=NPER(15%/12;;-1000;2107,18;1)
Para pagamento único não fará diferença no cálculo final.
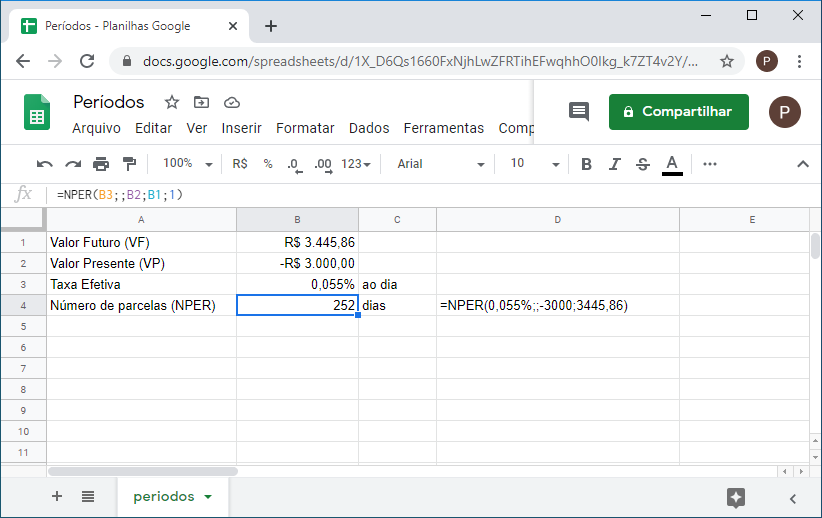
3. Você faz um investimento que paga 0,055% ao dia de juros. Se o valor investido inicialmente foi de R$3.000 e o valor resgatado foi de R$ 3.455,86, quanto tempo o dinheiro ficou investido?
Considerando que a taxa é cotada como sendo diária, não há necessidade de proporcioná-la, portanto o valor futuro é:
=NPER(0,055%;;-3000;3445,86) Resultando 252 dias
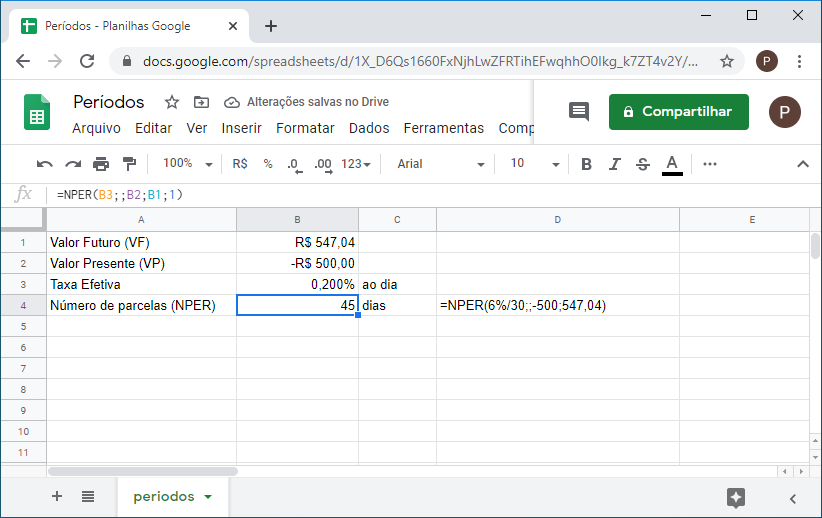
4. Sabendo que a taxa cobrada para um empréstimo é 6% ao mês, se o valor do empréstimo foi de R$500 com juros aplicados diariamente, em quanto tempo o empréstimo foi pago se o valor pago foi de R$547,04
=NPER(6%/30;;-500;547,04) Resultando
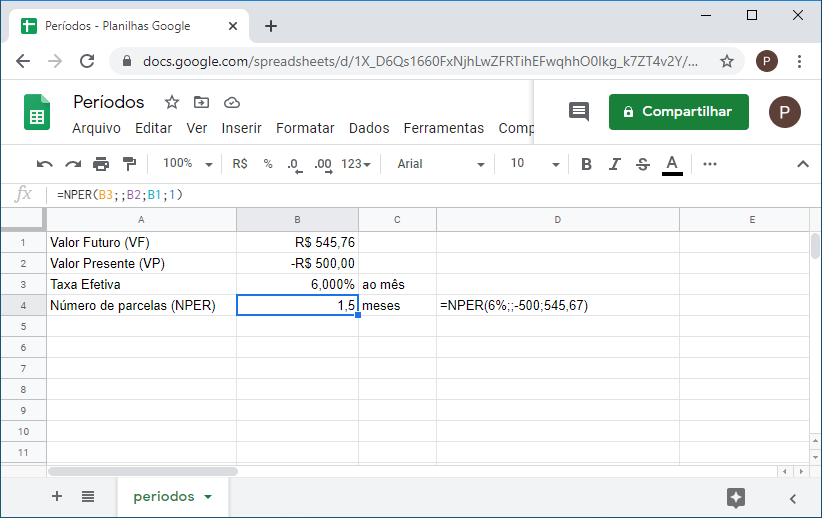
5. Utilizando o mesmo exemplo anterior, quanto tempo levou se a capitalização foi mensal e o valor resgatado foi de R$545,67?
=NPER(6%;;-500;545,67)
O resultado final representa 1 mês e meio ou 45 dias.
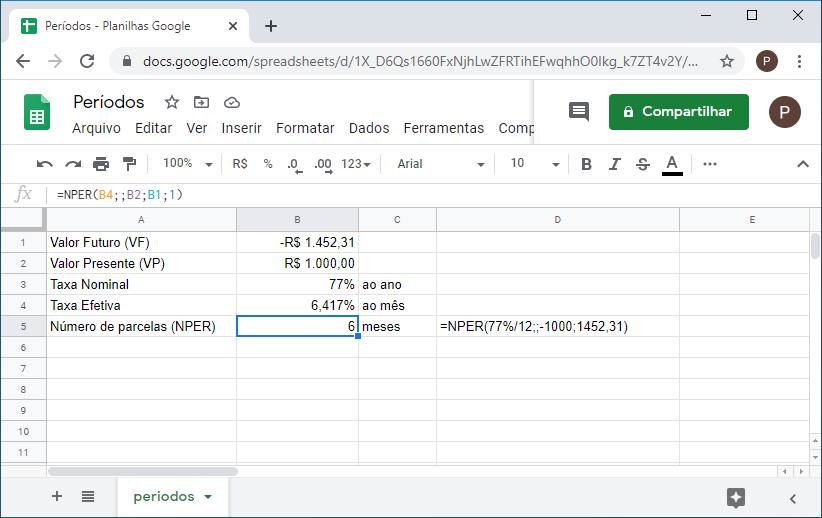
6. Sabendo que a taxa anual nominal é de 77% para empréstimos pessoais, por um empréstimo de R$1.000 você paga R$ 1.452,31. Se a capitalização foi mensal, qual foi o período do empréstimo?
Como a taxa é cotada por ano, precisamos proporcioná-la para o tipo de capitalização.
=NPER(77%/12;;-1000;1452,31)
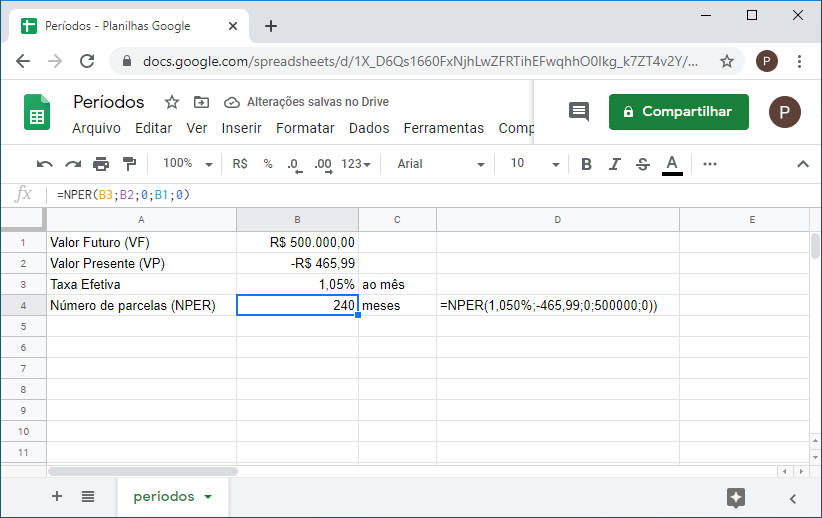
7. Se você dispõe de R$465,99 para depositar em um fundo que paga 1,05% ao mês, quantos depósitos mensais terá que fazer para acumular R$ 500.000,00?
=NPER(1,050%;-465,99;0;500000;0))
Ou seja 20 anos
Pagamentos e Taxa
Taxa Nominal e Efetiva
Taxas podem causar muita confusão. Há várias formas de se cotar uma taxa: elas podem ser nominais anuais, semestrais, mensais, diárias, etc. Podem ser efetivas anuais, trimestrais, mensais, semanais, diárias, etc. Ou podem ainda ser equivalentes. É importante compreender o tipo de taxa sendo utilizada, pois a planilha não tem um método de verificação de taxas. O que você precisa ter em mente quando utilizar as funções da planilha é que as taxas devem ser proporcionais à ocorrência do pagamento. Por exemplo, se alguém lhe passa uma taxa nominal anual de 10% a.a, mas a capitalização ocorre mensalmente você precisa proporcionar 10% por 12 (número de meses no ano). Se a taxa fosse 1% ao mês e capitalizada diariamente, você precisa proporcionar 1% por 21 dias úteis (ou a fração referente ao número de vezes que a taxa será capitalizada no mês).
Taxa Nominal
Taxa nominal é aquela que possui valor de face. Imagine uma nota de R$10, quanto ela vale? A resposta que parece ser óbvia é que uma nota de R$10 vale R$10. Mas será que vale mesmo? Uma nota de R$10 somente vale R$10 porque você acredita que ela vale os R$10, em outras palavras, o valor é fiduciário e mais nada. Quando uma passagem de ônibus passa de R$1,00 para R$2,00 os seus R$10 não valem mais a mesma coisa, embora seu valor de face continue o mesmo. Antes, ela pagava dez passagens de ônibus. Agora, ela paga apenas cinco passagens. Embora você saiba que a nota ainda tenha o mesmo valor de face, você também sabe que ela compra menos do que antes. Este valor de face é o seu valor nominal.
A taxa nominal nada mais é do que isso. É uma taxa que não é real. Se você fosse receber 1% de juros ao mês a taxa nominal para o ano seria 12% (12*1%); porém, esta não é a taxa realmente recebida. Desta forma, eu poderia dizer que você recebe 12% de juros ao ano, taxa nominal, mas até a realização da capitalização esta taxa tem apenas valor de face, pois não será este o valor recebido ou o valor real da taxa. Mas como reconhecer uma taxa nominal? E por que as pessoas falam de taxas nominais ao invés de efetivas?
Reconhecer um taxa nominal é bem simples. Procure apenas pelo valor de face do custo do dinheiro. Por exemplo, se você tem uma taxa mensal para pagamentos mensais, a taxa será efetiva, pois existe o “casamento” entre a proporção da taxa e o período. Se por outro lado a taxa é anual e o pagamento é mensal você estará observando uma taxa nominal (a menos que seja informado o contrário).
As pessoas utilizam taxas nominais pelo mesmo motivo que usamos as notas de R$10 quando elas já não possuem o mesmo valor que 10 anos atrás. Se cada nota no mercado representasse o seu valor naquele momento no tempo, a Casa da Moeda do Brasil teria que imprimir e distribuir notas a cada segundo, pois o processo de desvalorização é contínuo.
Colocando este parágrafo no contexto da taxa nominal, com uma taxa nominal cotada para o ano inteiro, você pode proporcionar para qualquer período dentro do ano para encontrar a sua taxa efetiva, isto é, o quanto realmente custa o dinheiro. Caso contrário, você teria que prever todas as condições e combinações possíveis de taxas dentro do ano. Com uma taxa única para o ano, basta proporcionar para o período desejado quando ele surgir e se surgir.
Nas Planilhas do Google, a taxa nominal é calculada utilizando a função: NOMINAL(taxa_efetiva;periodos_ao_ano) onde taxa_efetiva é a taxa de juros efetiva e periodos_ao_ano é o número de períodos compostos por ano.
Observações:
- N_per_ano é truncado para que apareça como um número inteiro.
- Se qualquer um dos argumentos não for numérico, NOMINAL retornará o valor de Erro:.
- Se taxa_efetiva ≤ 0 ou se N_per_ano < 1, NOMINAL retornará o valor de Erro:.
Ou seja, primeiro argumento é a taxa efetiva e o segundo o número de períodos que são compostos no ano. O período pode ser qualquer coisa. Contudo, se a taxa não estiver na mesma base o resultado não será o esperado.
Exemplos
Abaixo desenvolvo várias questões envolvendo taxas nominais.
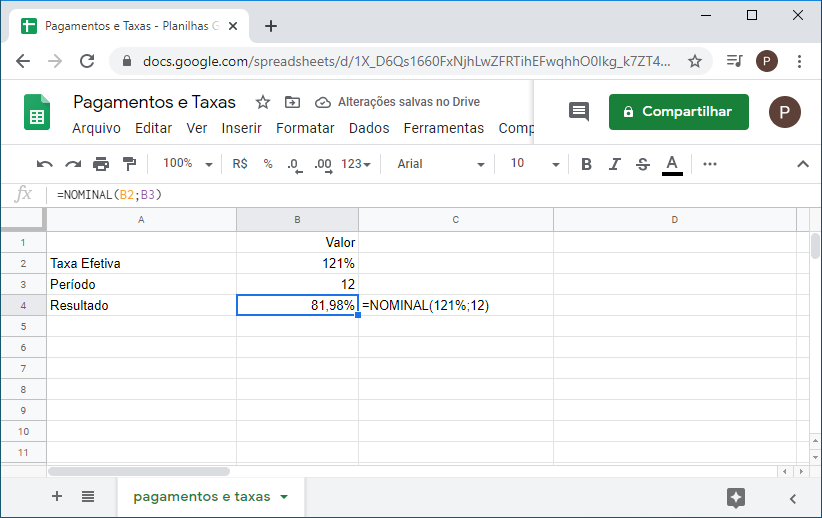
1. Você decide fazer o financiamento de um carro. Os juros efetivamente cobrados pela financeira somam 121% ao ano. Se o pagamento é mensal, qual a taxa nominal anual?
=NOMINAL(121%;12)
2. Se a taxa efetiva mensal é 1,5% qual a taxa nominal anual?
Nesse caso basta multiplicar por 12 a taxa efetiva mensal = 1,5%*12 = 18%
3. Você investe R$ 1.100,00 e recebe R$1.855,23 depois de 2 anos. Se a taxa de juros foi composta mensalmente, qual a taxa nominal anual deste investimento?
Primeiramente devemos calcular a taxa efetiva mensal desse investimento, para isso usamos a função taxa disponível na planilha.
A função TAXA retorna a taxa efetiva de juros por período. TAXA é calculada por interação e pode não chegar a uma solução. Se os resultados sucessivos da TAXA não convergirem para 0,0000001 depois de 20 iterações, a TAXA retornará com valor de Erro.
A fórmula da taxa é TAXA(numero_de_periodos; pagamento_por_periodo; valor_atual; [valor_futuro]; [fim_ou_inicio]; [taxa_estimada]), onde:
- numero_de_periodos é o número total de períodos ou o número sucessivo de pagamentos ou recebimentos em uma série de pagamentos;
- pagamento_por_periodo é o pagamento feito em cada período em uma série de pagamentos, e não pode mudar durante a vigência;
- valor_atual é o é o valor presente ou valor atual de uma série de pagamentos futuros;
- valor_futuro é um item opcional e significa o valor final, que você deseja obter depois do último pagamento, se o valor_futuro for omitido, será considerado 0, ou ainda o valor futuro restante após o pagamento final;
- fim_ou_inicio também é um item opcional e que indica se os pagamentos são feitos no final (“0”) ou no início (“1”) de cada período;
- taxa_estimada também é um item opcional e significa uma estimativa para a taxa de juros, se você omitir estimativa, este argumento será considerado 10%. Se a TAXA não convergir, atribua valores diferentes para estimativa. Em geral, TAXA converge se a estimativa estiver entre 0 e 1.
Então, resolvendo exemplo acima temos que:
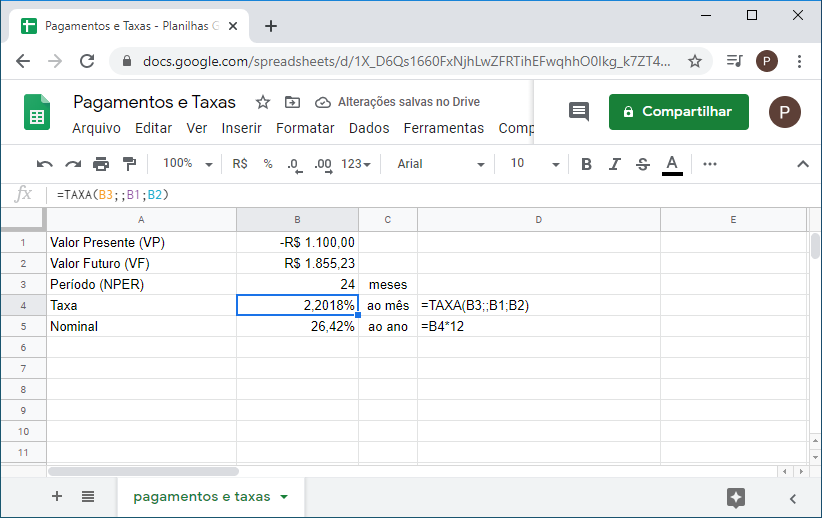
Para calcular a taxa nominal anual multiplica-se por 12, totalizando 26,4216% ao ano.
4. Um investimento de 21 dias retorna R$775,61 por um investimento inicial de R$716,00. Qual a taxa nominal mensal?
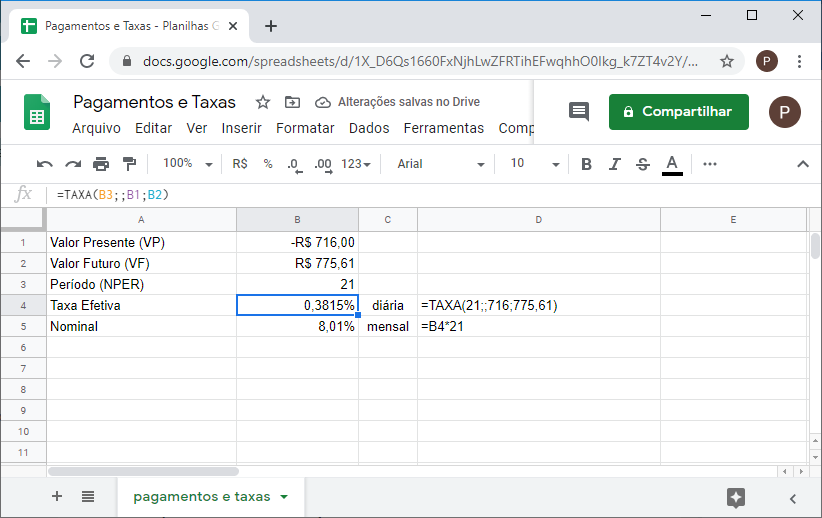
Para calcular a taxa nominal mensal multiplica-se por 21, totalizando 8,0122% ao mês.
OBS: Neste exemplo, um erro comum ocorre. Geralmente, a tendência é tratar os valores presente e futuro com sendo positivo. Porém, ao fazer isso cometemos um erro. O fluxo de caixa não pode ser somente positivo, devemos ter uma entrada e uma saída de caixa.
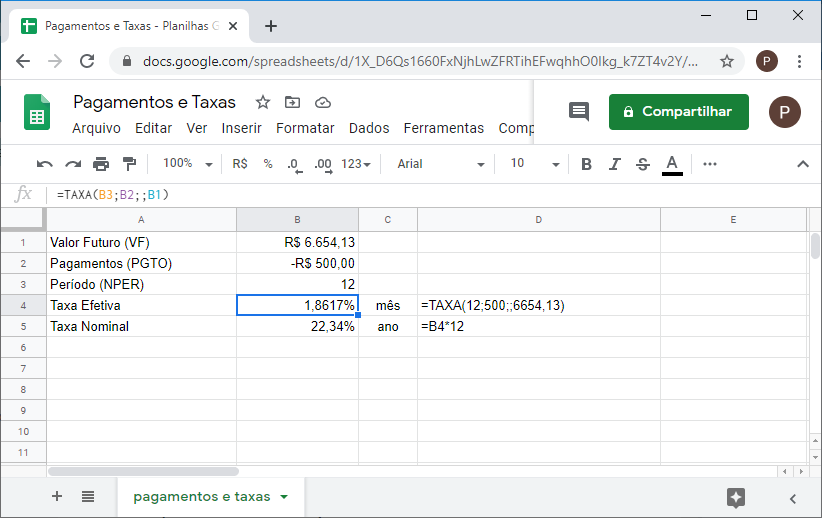
5. Você deposita mensalmente a quantia de R$500,00 por doze meses. Quando você finalmente resgata o dinheiro, o montante recebido é de R$6.654,13. Qual a taxa nominal anual aplicada neste investimento?
Taxa Efetiva
Taxa Efetiva, como o nome sugere, é a taxa efetivamente paga ou recebida. Se um investimento paga uma taxa mensal de 1% e este é o valor final recebido; então, esta é sua taxa efetiva. Por outro lado, se a taxa fosse cotada como sendo anual nominal, digamos, 12%; então, a sua taxa efetiva anual é dada por:
EFETIVA = ( 1 + i / m )m – 1
Onde m é o número de vezes que i (a taxa nominal) é composta no período. Se a taxa é composta 12 vezes por ano, então:
EFETIVA = ( 1 + 0,12 / 12 )12 – 1
EFETIVA = 12,6825% ao ano
Na planilha, a taxa efetiva é calculada utilizando a função EFETIVA(taxa_nominal; periodos_ao_ano). Como o processo é o oposto da taxa nominal, devemos inserir a taxa nominal como o primeiro argumento da função.
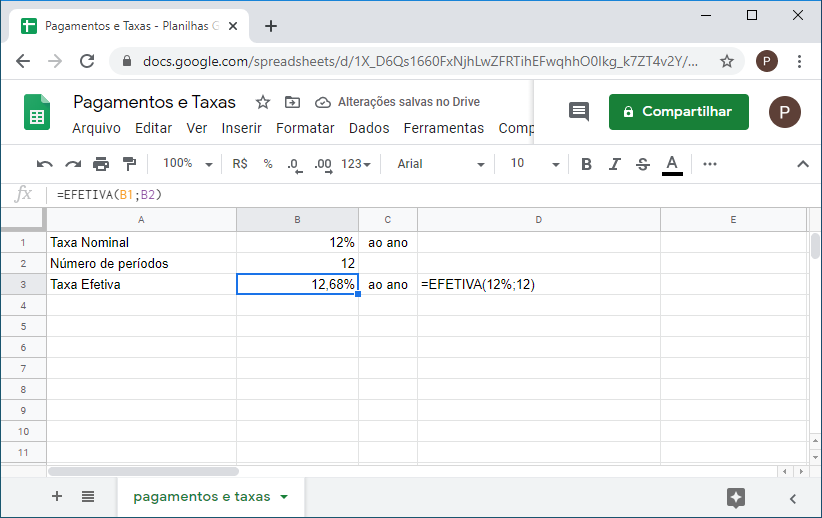
A importância da taxa nominal pode ser vista agora. No exemplo acima a taxa efetiva para capitalização mensal é 12,68%. Se a capitalização fosse diária, com a mesma taxa nominal podemos encontrar a taxa anual efetiva:
EFETIVA = ( 1 + 0,12 / 252 )252 – 1 => taxa efetiva 12,7464% ano
Para resolver na planilha basta substituir 12 por 252 (dias efetivos no ano) na atividade anterior.
Como podemos ver, para cada capitalização (valor m) há uma taxa efetiva diferente. Porém, todas estas taxas convergem para uma única taxa nominal no ano. Isso facilita em muito o nosso cálculo, pois temos apenas uma variável para manipular. Imagine a situação onde você deseja elaborar uma tabela de capitalização. Se você tivesse que definir uma taxa efetiva para cada período você teria mais trabalho do que definir uma taxa única para o ano e proporcioná-la conforme surgir à necessidade.
Abaixo desenvolvemos algumas questões envolvendo taxas efetivas.
1. Um investimento oferece uma taxa nominal 1% ao mês. Se este valor é composto diariamente, qual a taxa efetiva para o mês? Assuma 21 dias úteis no mês.
Observe que a taxa é cotada para o mês. Considerando um mês de 21 dias úteis podemos facilmente encontrar a taxa efetiva para o mês:
= EFETIVA(1%;21)
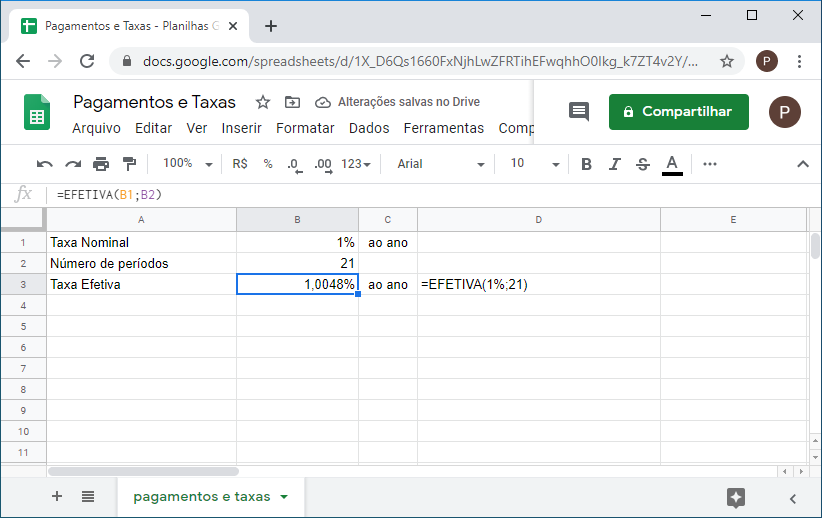
Que tem o mesmo efeito que:
( 1 + 0,01 / 21 )21 – 1=> taxa efetiva 1,0048% mês
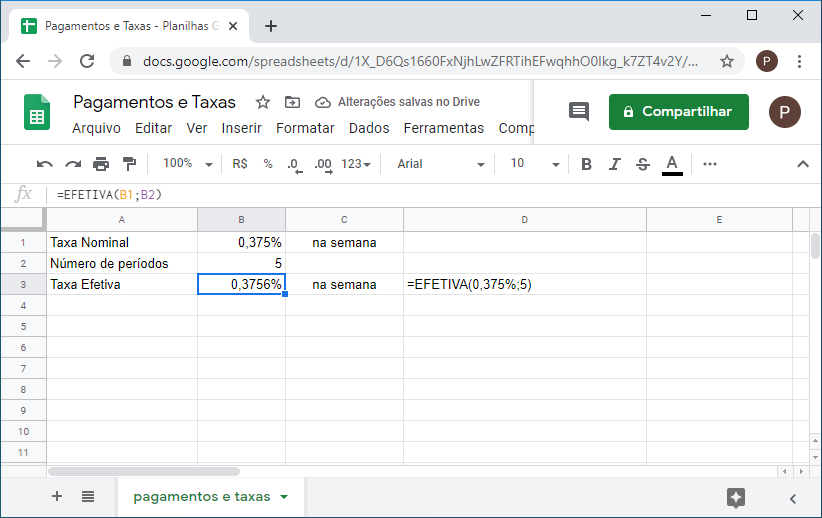
2. Um investimento oferece uma taxa diária de 0,075%. Qual a taxa efetivamente recebida na sexta-feira se o investimento foi feito na segunda-feira.
A taxa nominal no período poder ser calculada como 0,075*5 (5 dias) = 0,375
= EFETIVA(0,075%*5;5)
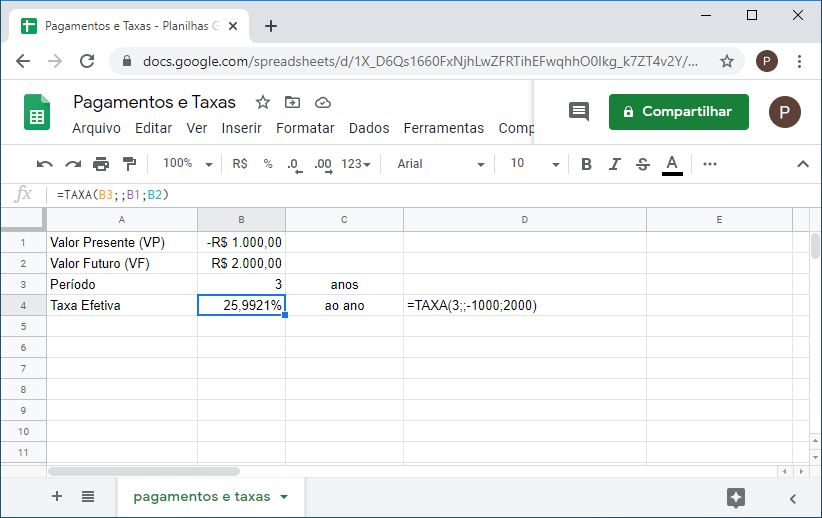
3. Um investimento inicial de R$1.000,00 dobra em três anos. Sabendo que a capitalização foi mensal, qual foi à taxa efetiva anual?
Para resolver essa atividade usamos a função TAXA(NPER;PGTO;VP;VF;Tipo;Estimativa).
4. Você faz um empréstimo pessoal de R$5.000,00 que será liquidado em 36 parcelas de R$256,35. O gerente do banco informa que a taxa efetiva do empréstimo é de 45,33%. Esta informação está correta?
Utilizando a função TAXA para resolver o problema, temos:
=TAXA(36;-256,35;5000;0;0)*12
=EFETIVA_ADD(TAXA(36;-256,35;5000;0;0)*12;12)
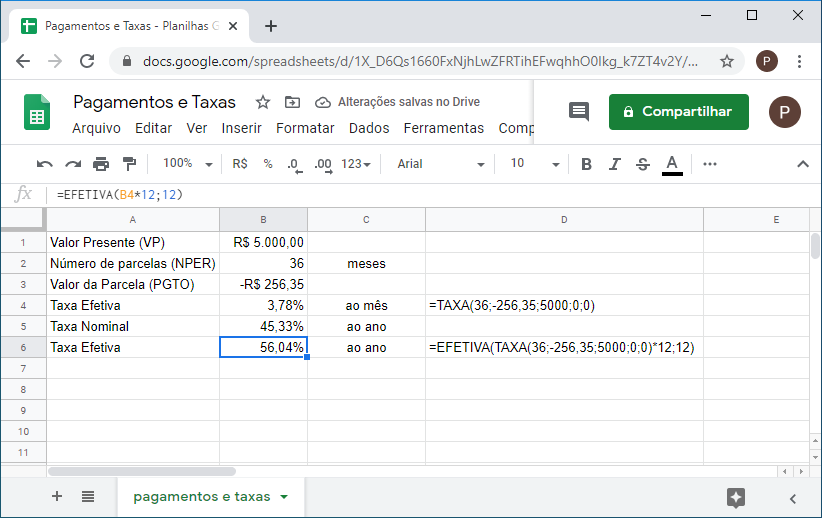
A taxa informada pelo gerente é a taxa nominal, a taxa efetiva é de 56,0435% ao ano.
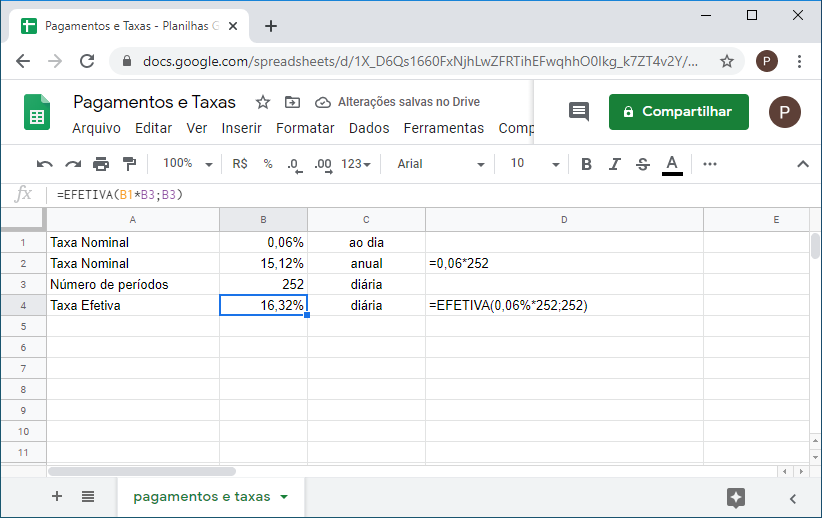
5. Um investimento qualquer paga uma taxa diária de 0,06%. Considerando um ano de 252 dias úteis, qual a taxa efetivamente recebida no final de um ano?
=EFETIVA(0,06%*252;252)