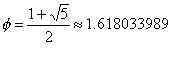O Misterioso Número de Ouro
O Número de Ouro é um número irracional, misterioso e enigmático que nos surge numa infinidade de elementos da natureza na forma de uma razão. O número de ouro foi estudado, pelos Gregos num contexto geométrico. Euclides dividiu um segmento de reta AB em duas partes tais que
Ι AP Ι ÷ Ι PB Ι = Ι AB Ι ÷ Ι AP Ι ou x ÷ 1 = (x+1) ÷ x
____________._____________
A P B
A razão é o número de ouro e o seu valor é:
Figura: Partenon – Templo em Atenas, Grécia
A notação para este número, Φ (Phi maiúsculo), é a inicial do nome de Fídias que foi escultor e arquiteto encarreg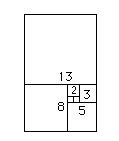
ado da construção do Pártenon, em Atenas onde o Φ aparece na a razão entre a largura e a altura da fachada. Um exemplo deste fato é que se desenharmos um retângulo cujos lados tenham uma razão ente si igual ao número de Ouro este pode ser dividido num quadrado e noutro retângulo em que este tem também ele, a razão entre os dois lados igual ao número de Ouro (figura à esquerda). Este processo pode ser repetido indefinidamente mantendo-se a razão constante.
Um dos grandes divulgadores do número de ouro foi Fibonacci. Com o famoso problema dos coelhos publicado no seu livro Liber Abaci, a sequência de números de Fibonacci:
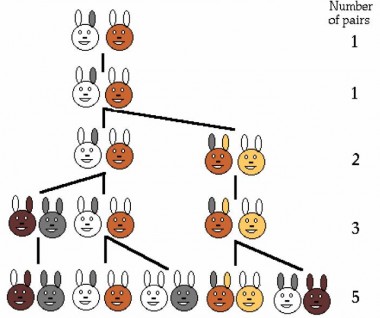
Suponha-se um par de coelhos recém-nascidos, uma fêmea e um macho, colocados num jardim. Os coelhos podem acasalar ao fim de um mês de vida, de tal forma que ao fim do segundo mês pode nascer um novo par de coelhos. Suponha que os seus coelhos não morrem e que, cada mês a partir do segundo mês de vida, cada casal origina um novo casal. Quantos pares de coelhos haverá ao fim de um ano?
A sucessão de Fibonacci e o número de ouro.
Números de Fibonacci:1, 1, 2, 3, 5, … Qual será o seguinte? Fn+1= Fn+Fn-1
Razões: 1/1, 2/1, 3/2, 5/3, f (n+1)/f (n) → número de ouro (1,61803 …)
Beleza também é questão de matemática
Um artista que utilizava muito o número de ouro é Leonardo Da Vinci. Ele montou uma tabela de proporção do corpo humano, onde o umbigo divide a altura do corpo em dois segmentos que estão na razão de ouro. O ombro divide a distância entre as extremidades dos dedos (braços abertos perpendicularmente ao corpo) em dois segmentos também. Os seres mais belos possuem razão próxima da razão de ouro.
E você o quanto estás próximo da beleza?
Na natureza a presença da razão áurea pode ser direta ou encontrar-se camuflada ou ainda associada à sucessão de Fibonacci.
Nos girassóis da família compõem as sementes formam dois conjuntos de espirais logarítmicas com sentidos diferentes. Cada conjunto tem um número de sementes e os dois conjuntos tem dois números de sementes que são consecutivos de Fibonacci.
O mesmo acontece com as pinhas:
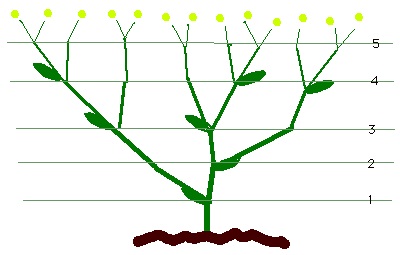
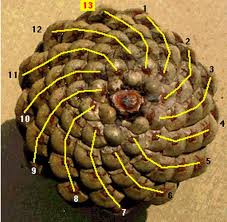Podemos afirmar que o modelo de desenvolvimento das plantas pode ser relacionado com os números de Fibonacci.
Existe, por exemplo, uma planta de nome Euforbia, que tem duas sépalas grandes, três pequenas, cinco pétalas e oito estames.
Como construir um retângulo de ouro?
Se desenharmos um retângulo cujos lados tenham uma razão entre si igual ao número de ouro (retângulo de ouro), este pode ser dividido num quadrado e noutro retângulo de ouro.
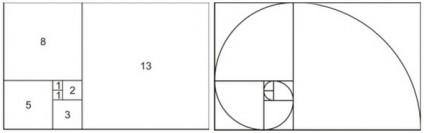Se unirmos os quartos de circunferência de todos os quadrados vamos obter uma espiral, chamada espiral dourada.
Fonte:
Centro de Matemática da Universidade do Porto